4 Exercises
For a rigid body with mass \(m = 100\) kg and center of gravity located at \(\vec{r}_G = [0.1, -0.15, 0.2]^T\) m in BCS, calculate both the upper right and lower left \(3 \times 3\) blocks of the rigid body mass matrix \(\boldsymbol{M}_{RB}\). Verify that they are negative transposes of each other.
Given a rigid body with principal moments of inertia \(I_x^G = 20\) kg⋅m², \(I_y^G = 25\) kg⋅m², \(I_z^G = 30\) kg⋅m² about its center of gravity, and products of inertia \(I_{xy}^G = 2\), \(I_{xz}^G = -3\), \(I_{yz}^G = 1\) kg⋅m², construct the complete inertia tensor \(\boldsymbol{I}_G\). Is the resulting matrix symmetric?
A rigid body has angular velocity \(\vec{\omega} = [0.1, 0.2, 0.3]^T\) rad/s. Calculate the skew-symmetric matrix \(\boldsymbol{S}(\vec{\omega})\) and verify the properties:
\(\boldsymbol{S}(\vec{\omega})^T = -\boldsymbol{S}(\vec{\omega})\),
\(\boldsymbol{S}(\vec{\omega})\vec{\omega} = \vec{0}\),
\(\boldsymbol{S}(\vec{\omega})\boldsymbol{S}(\vec{\omega}) = \vec{\omega}\vec{\omega}^T - \|\vec{\omega}\|^2\boldsymbol{I}_{3\times3}\).
For a rigid body with mass \(m = 500\) kg and center of gravity at \(\vec{r}_G = [0.3, 0.5, -0.2]^T\) m in BCS, use the parallel axis theorem to:
Calculate \(\boldsymbol{S}(\vec{r}_G)\boldsymbol{S}(\vec{r}_G)\),
Determine the additional inertia terms needed to transform \(\boldsymbol{I}_G\) to \(\boldsymbol{I}_O\),
Show that the resulting matrix is symmetric.
A rigid body has linear velocity \(\vec{v} = [1, 2, -1]^T\) m/s and angular velocity \(\vec{\omega} = [0.1, 0.2, -0.15]^T\) rad/s. Calculate:
The acceleration term \(\vec{\omega} \times \vec{v}\) using cross product,
The same term using the skew-symmetric matrix \(\boldsymbol{S}(\vec{\omega})\),
Verify both methods give the same result.
A rigid body has mass \(m = 200\) kg and center of gravity at \(\vec{r}_G = [0.2, -0.1, 0.15]^T\) m in BCS. If it experiences forces \(\vec{F}_1 = [100, -50, 25]^T\) N at point \(\vec{r}_1 = [0, 0, 0]^T\) m and \(\vec{F}_2 = [-30, 40, -20]^T\) N at point \(\vec{r}_2 = [0.1, 0.1, 0.1]^T\) m (both in BCS), calculate:
The total force,
The moment about O,
The moment about G.
For a rigid body with angular velocity \(\vec{\omega} = [0.5, -0.3, 0.2]^T\) rad/s and inertia tensor \(\boldsymbol{I}_G\) with principal moments \([20, 25, 30]\) kg⋅m² and products of inertia \(I_{xy}^G = I_{yz}^G = I_{xz}^G = 5\) kg⋅m², calculate:
\(\boldsymbol{I}_G\vec{\omega}\),
\(\vec{\omega} \times \boldsymbol{I}_G\vec{\omega}\),
The rotational kinetic energy \(\frac{1}{2}\vec{\omega}^T\boldsymbol{I}_G\vec{\omega}\).
Given a rigid body with mass \(m = 300\) kg, \(\vec{r}_G = [0.25, -0.15, 0.1]^T\) m, and \(\boldsymbol{I}_G = \text{diag}(40, 45, 50)\) kg⋅m², calculate:
The complete \(6 \times 6\) rigid body mass matrix \(\boldsymbol{M}_{RB}\),
Show that it is symmetric,
Calculate its determinant.
A rigid body has linear velocity \(\vec{v} = [2, 1, -1]^T\) m/s, angular velocity \(\vec{\omega} = [0.1, -0.2, 0.15]^T\) rad/s, and center of gravity at \(\vec{r}_G = [1, -0.5, 0.3]^T\) m. Calculate:
The velocity of G in BCS,
The acceleration terms \(\vec{\omega} \times \vec{v}\) and \(\vec{\omega} \times (\vec{\omega} \times \vec{r}_G)\),
The total acceleration of G if \(\dot{\vec{v}} = [0.1, 0.2, -0.1]^T\) m/s² and \(\dot{\vec{\omega}} = [0, 0.1, 0]^T\) rad/s².
For a rigid body with \(\vec{\omega} = [0.2, -0.1, 0.3]^T\) rad/s and \(\vec{r}_G = [0.5, -0.2, 0.1]^T\) m, calculate:
The centripetal acceleration term \(\vec{\omega} \times (\vec{\omega} \times \vec{r}_G)\) using cross products,
The same term using skew-symmetric matrices,
Show that both methods yield identical results.
A rigid body has mass \(m = 400\) kg, center of gravity at \(\vec{r}_G = [0.3, -0.1, 0.2]^T\) m, and inertia tensor \(\boldsymbol{I}_G\) with principal moments \([50, 60, 45]\) kg⋅m² and products of inertia \(I_{xy}^G = I_{yz}^G = I_{xz}^G = 8\) kg⋅m². If it experiences force \(\vec{F} = [200, -100, 50]^T\) N and moment \(\vec{M} = [20, -10, 5]^T\) N⋅m at O, with initial velocities \(\vec{v} = [1, -0.5, 0.2]^T\) m/s and \(\vec{\omega} = [0.1, 0, -0.1]^T\) rad/s, calculate:
The complete mass matrix \(\boldsymbol{M}_{RB}\),
All acceleration-dependent terms,
Solve for \(\dot{\vec{v}}\) and \(\dot{\vec{\omega}}\).
For a rigid body of mass \(m = 100\) kg, center of gravity at \(\vec{r}_G = [0.1, -0.1, 0.2]^T\) m, and inertia tensor \[\begin{align*} \boldsymbol{I}_G = \begin{bmatrix} 30 & 4 & -2 \\ 4 & 35 & 3 \\ -2 & 3 & 40 \end{bmatrix} \text{ kg⋅m²} \end{align*}\] angular velocity \(\vec{\omega} = [0.1, 0.2, 0.3]^T\) rad/s, and linear velocity \(\vec{v} = [1, -0.5, 0.2]^T\) m/s:
Derive the complete expression for \(\boldsymbol{C}_{RB}(\{v\})\{v\}\),
Show that \(\{v\}^T\boldsymbol{C}_{RB}(\{v\})\{v\} = 0\),
Explain the physical significance of this property.
Given a rigid body with mass \(m = 600\) kg, \(\vec{r}_G = [0.2, 0.1, -0.1]^T\) m, and inertia tensor \[\begin{align*} \boldsymbol{I}_G = \begin{bmatrix} 500 & -25 & -30 \\ -25 & 600 & 35 \\ -30 & 35 & 650 \end{bmatrix} \text{ kg⋅m²} \end{align*}\]
Derive the complete expression for the Coriolis matrix \(\boldsymbol{C}_{RB}(\{v\})\),
Show that \(\dot{\boldsymbol{M}}_{RB} - 2\boldsymbol{C}_{RB}(\{v\})\) is skew-symmetric,
Explain why this property is important for energy conservation.
Hint: What should be the rate of change of kinetic energy (\(\dot{T}\)) for a rigid body that is not subject to any external forces (i.e. \(\{\tau_{RB}\}=0\))? Remember that the total kinetic energy of a rigid body is given by \(T = \frac{1}{2} \vec{v}^T \boldsymbol{M}_{RB} \vec{v}\)
A marine vehicle has the following inertia tensors measured about its center of gravity (G) and about the origin of BCS (O): \[\begin{align*} \boldsymbol{I}_G = \begin{bmatrix} 400 & -20 & -15 \\ -20 & 450 & 25 \\ -15 & 25 & 500 \end{bmatrix} \text{ kg⋅m²}, \quad \boldsymbol{I}_O = \begin{bmatrix} 410 & -10 & -25 \\ -10 & 475 & 30 \\ -25 & 30 & 525 \end{bmatrix} \text{ kg⋅m²} \end{align*}\] If the mass of the vehicle is \(m = 500\) kg:
Determine the coordinates of the center of gravity \(\vec{r}_G = [x_G, y_G, z_G]^T\)
Calculate \(\boldsymbol{S}(\vec{r}_G)\boldsymbol{S}(\vec{r}_G)\) and verify it matches with \(\frac{1}{m}(\boldsymbol{I}_O - \boldsymbol{I}_G)\)
Programming Exercise: A marine vehicle with mass \(m = 1000\) kg, center of gravity at \(\vec{r}_G = [0.2, 0, 0.1]^T\) m, and inertia tensor \[\begin{align*} \boldsymbol{I}_G = \begin{bmatrix} 800 & 0 & -50 \\ 0 & 1200 & 0 \\ -50 & 0 & 1000 \end{bmatrix} \text{ kg⋅m²} \end{align*}\] starts from rest with initial orientation \(\phi = 20^{\circ}\), \(\theta = 30^{\circ}\), \(\psi = 45^{\circ}\) and experiences time-varying forces and moments for \(25\) seconds:
- \(\vec{F}(t) = [500\cos\left(\frac{\pi t}{50}\right), 200\sin\left(\frac{\pi t}{50}\right), -100]^T\) N
- \(\vec{M}(t) = [50\cos\left(\frac{\pi t}{50}\right), 30\sin\left(\frac{\pi t}{50}\right), 20]^T\) N⋅m
- Derive the complete equations of motion including all Coriolis terms
- Using RK45 integration, determine the final pose and velocities (use may explore different solvers in
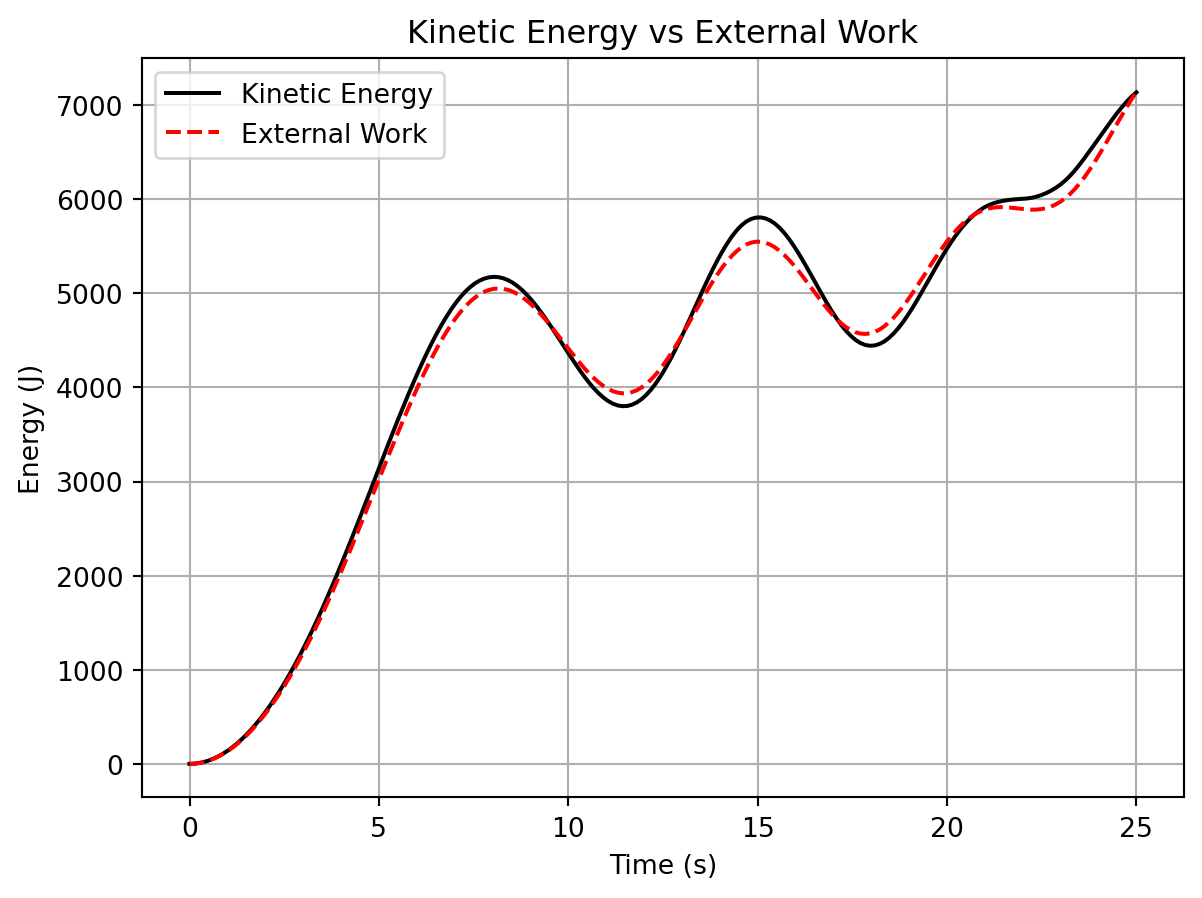
scipy.integrate.solve_ivp) - Plot the time history of kinetic energy and verify its rate of change equals the work done by the external forces and moments.
Answer Key
\(\boldsymbol{M}_{12} = \begin{bmatrix} -0.00 & 20.00 & 15.00 \\ -20.00 & -0.00 & 10.00 \\ -15.00 & -10.00 & -0.00 \end{bmatrix}\) kg⋅m
\(\boldsymbol{M}_{21} = \begin{bmatrix} 0.00 & -20.00 & -15.00 \\ 20.00 & 0.00 & -10.00 \\ 15.00 & 10.00 & 0.00 \end{bmatrix}\) kg⋅m \(= -\boldsymbol{M}_{12}^T\)
\(\boldsymbol{I}_{G} = \begin{bmatrix} 20.00 & -2.00 & 3.00 \\ -2.00 & 25.00 & -1.00 \\ 3.00 & -1.00 & 30.00 \end{bmatrix}\) kg⋅m²
- \(\boldsymbol{S}(\vec{\omega}) = \begin{bmatrix} 0.00 & -0.30 & 0.20 \\ 0.30 & 0.00 & -0.10 \\ -0.20 & 0.10 & 0.00 \end{bmatrix}\)
\(\boldsymbol{S}(\vec{r}_G) \boldsymbol{S}(\vec{r}_G) = \begin{bmatrix} -0.29 & 0.15 & -0.06 \\ 0.15 & -0.13 & -0.10 \\ -0.06 & -0.10 & -0.34 \end{bmatrix}\) kg⋅m²
\(\boldsymbol{I}_{O} - \boldsymbol{I}_{G} = \begin{bmatrix} 145.00 & -75.00 & 30.00 \\ -75.00 & 65.00 & 50.00 \\ 30.00 & 50.00 & 170.00 \end{bmatrix}\) kg⋅m²
\(\vec{\omega} \times \vec{v} = \begin{bmatrix} 0.10 \\ -0.05 \\ 0.00 \end{bmatrix}\) m/s²
\(\boldsymbol{F}_{total} = \begin{bmatrix} 70.00 \\ -10.00 \\ 5.00 \end{bmatrix}\) N
\(\boldsymbol{M}_{O} = \begin{bmatrix} -6.00 \\ -1.00 \\ 7.00 \end{bmatrix}\) N⋅m
\(\boldsymbol{M}_{G} = \begin{bmatrix} -7.00 \\ -10.50 \\ 2.00 \end{bmatrix}\) N⋅m
\(\boldsymbol{I}_G \vec{\omega} = \begin{bmatrix} 10.50 \\ -11.00 \\ 5.00 \end{bmatrix}\) kg⋅m²/s
\(\vec{\omega} \times (\boldsymbol{I}_G \times \vec{\omega}) = \begin{bmatrix} 0.70 \\ -0.40 \\ -2.35 \end{bmatrix}\) kg⋅m²/s²
\(T_R = 4.775\) J
Mass matrix \(\boldsymbol{M}_{RB} = \begin{bmatrix} 300.00 & 0.00 & 0.00 & -0.00 & 30.00 & 45.00 \\ 0.00 & 300.00 & 0.00 & -30.00 & -0.00 & 75.00 \\ 0.00 & 0.00 & 300.00 & -45.00 & -75.00 & -0.00 \\ 0.00 & -30.00 & -45.00 & 49.75 & 11.25 & -7.50 \\ 30.00 & 0.00 & -75.00 & 11.25 & 66.75 & 4.50 \\ 45.00 & 75.00 & 0.00 & -7.50 & 4.50 & 75.50 \end{bmatrix}\)
Is symmetric: True
Determinant: \(243 \times 10^{10}\)
Velocity of G \(\{v_G\} = \begin{bmatrix} 2.02 \\ 1.12 \\ -0.85 \end{bmatrix}\) m/s
Acceleration terms: \(\boldsymbol{\omega} \times \boldsymbol{v} = \begin{bmatrix} 0.05 \\ 0.40 \\ 0.50 \end{bmatrix}\) m/s²
\(\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r}_G) = \begin{bmatrix} -0.05 \\ -0.01 \\ 0.01 \end{bmatrix}\) m/s²
Total acceleration of G \(\{a_G\} = \begin{bmatrix} 0.13 \\ 0.59 \\ 0.32 \end{bmatrix}\) m/s²
Centripetal acceleration vector is given by:
\(\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r}_G) = \begin{bmatrix} -0.04 \\ 0.01 \\ 0.03 \end{bmatrix}\) m/s²
\(\dot{v} = \begin{bmatrix} 0.64 \\ -0.20 \\ 0.02 \end{bmatrix}\) m/s² and \(\dot{\omega} = \begin{bmatrix} 0.05 \\ -0.54 \\ 0.25 \end{bmatrix}\) rad/s²
\(\boldsymbol{C}_{RB}\{v\} = \begin{bmatrix} 18.10 \\ 30.40 \\ -26.30 \\ -3.46 \\ 5.97 \\ 5.04 \end{bmatrix}\)
\(\{v\}^T \boldsymbol{C}_{RB}\{v\} = 0.00\)
This property shows that the Coriolis forces and moments \(\boldsymbol{C}_{RB}\{v\}\) does no work preserving energy in the absence of external forces
\(\dot{\boldsymbol{M}}_{RB} - 2\boldsymbol{C}_{RB} = \begin{bmatrix} -0.0 & -0.0 & -0.0 & 0.0 & -2364.0 & -3516.0 \\ -0.0 & -0.0 & -0.0 & 2364.0 & 0.0 & -4740.0 \\ -0.0 & -0.0 & -0.0 & 3516.0 & 4740.0 & 0.0 \\ 0.0 & -2364.0 & -3516.0 & 0.0 & 779.2 & -690.8 \\ 2364.0 & 0.0 & -4740.0 & -779.2 & 0.0 & 43.2 \\ 3516.0 & 4740.0 & 0.0 & 690.8 & -43.2 & 0.0 \end{bmatrix}\)
Is Property verified: True
The skew-symmetry of \(\dot{\boldsymbol{M}}_{RB} - 2\boldsymbol{C}_{RB}\) ensures that the rate of change of kinetic energy is zero when there are no external forces or moments.
Two possible solutions exist and both are valid.
Solution 1: \(r_G = \begin{bmatrix} 0.20 \\ -0.10 \\ 0.10 \end{bmatrix}\)
Solution 2: \(r_G = \begin{bmatrix} -0.20 \\ 0.10 \\ -0.10 \end{bmatrix}\)